

Next: 5 Differences Between Computer
Up: 4 Surface Normal Vector
Previous: 4.1 Vector treatment
Combining Equations 1, 2 and 3,
we obtain Equation 5.
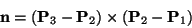 |
(5) |
Expanding this into the individual components, and using the definition of vector
cross-product, we obtain the three Equations 6 to 8.
In order to normalise these values, we find the scalar value 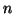 , using
the values for
, using
the values for 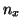 ,
, 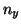 and
and 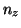 found in Equations
6 to 8.
found in Equations
6 to 8.
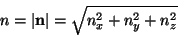 |
(9) |
We now use this normalisation factor to find the normalised versions of Equations
6 to 8.
The values 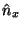 ,
, 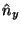 and
and 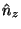 given
in Equations 10 to 12 are now the
given
in Equations 10 to 12 are now the
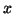 ,
, 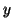 and
and 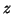 coordinates of the normalised surface normal
to the triangle with vertices
coordinates of the normalised surface normal
to the triangle with vertices
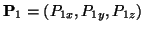 ,
,
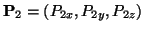 and
and
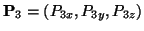 .
.


Next: 5 Differences Between Computer
Up: 4 Surface Normal Vector
Previous: 4.1 Vector treatment
Kevin Pulo
2000-08-22
![]() , using
the values for
, using
the values for ![]() ,
, ![]() and
and ![]() found in Equations
6 to 8.
found in Equations
6 to 8.