Assume we want to develop a Graphical User Interface for a control station in an electric power station. The single elements, like turbines, pipes and electrical installations are shown on a screen. For each power station element we derive a special class from the shape class in section 2 to represent its look on the screen. The class hierarchy could look like this:

Figure 4: Example shape class hierarchy
We store all shapes that are shown on a certain screen in the appropriate shape-container, e.g. all turbine objects that are shown on the main screen in a turbine-container. When the screen is called, the containers are used to draw a representation of the appropriate part of the power station.
In C++ one could use an array:
turbine main_screen_turbines [max_size];
where max_size is the maximum number of turbine objects that can be stored in the main_screen_turbines array.
When you use STL, you would choose this:
#include <vector.h>
typdef int turbine; // so we don´t have to define the turbine class
int main() {
vector<turbine> main_screen_turbines;
return 0;
}
Note: To make this little example run you have to read section 3.3 on how to compile STL programs. To use a vector in your program, include vector.h. In the following examples only the essential code lines are presented and most of the include stuff and the main function are omitted.
As you can see, you don't have to specify a maximum size for the vector, because the vector itself is able to dynamically expand its size. The maximum size the vector can reach - i.e. the maximum number of elements it is able to store - is returned by the member function max_size() of the vector class:
vector<turbine>::size_type max_size = main_screen_turbines.max_size();
Note: Many member functions described in the vector-section can be found among the rest of the STL containers, too. The description applies to those containers accordingly and will be referenced when discussing these containers.
size_type is an unsigned integral type, this could be for example unsigned long. The type that determines the size of the different containers is encapsulated by a typedef to abstract from the actual memory model used. For example:
typedef unsigned long size_type;
if the size is expressible by the built in type unsigned long.
STL abstracts from the specific memory model used by a concept named allocators. All the information about the memory model is encapsulated in the Allocator class. Each container is templatized (parametrized) by such an allocator to let the implementation be unchanged when switching memory models.
template <class T, template <class U> class Allocator = allocator>
class vector {
...
};
The second template argument is a default argument that uses the pre-defined allocator "allocator", when no other allocator is specified by the user. I will describe allocators in detail in section 4.5.
If you want to know the actual size of the vector - i.e. how many elements it stores at the moment - you have to use the size() member function:
vector<turbine> main_screen_turbines; vector<turbine>::size_type size = main_screen_turbines.size(); cout << "actual vector size: " << size;
Output: actual vector size: 0
Like size_type describes the type used to express the size of a container, value_type gives you the type of the objects that can be stored in it:
vector<float> v; cout << "value type: " << typeid (vector<float>::value_type).name();
Output: value type: float
Note: To use typeid include typeinfo.h
A container turns out useless if no object can be inserted into or deleted from it. The vector, of course, provides member functions to do these jobs and it does quite a bit more:
It is guaranteed that inserting and erasing at the end of the vector takes amortized constant time whereas inserting and erasing in the middle takes linear time.
As stated in [3], R-5, "In several cases, the most useful characterization of an algorithm's computing time is neither worst case time nor average time, but amortized time. [...] Amortized time can be a useful way to describe the time taken by an operation on some container in cases where the time can vary widely as a sequence of the operations is done, but the total time for a sequence of N operations has a better bound than just N times the worst-case time." To understand this, remember that a vector is able to automatically expand its size. This expansion is done, when an insert command is issued but no room is left in the storage allocated. In that case, STL allocates room for 2n elements (where n is the actual size of the container) and copies the n existing elements into the new storage. This allocation and the copying process take linear time. Then the new element is inserted and for the next n-1 insertions only constant time is needed. So you need O(n) time for n insertions, averaged over the n insert operations this results in O(1) time for one insert operation. This more accurately reflects the cost of inserting than using the worst-case time O(n) for each insert operation.
Of course amortized constant time is about the same overhead as you have when using C/C++ arrays but note that it is important to be about the same - and not more.
For the authors of STL complexity considerations are very important because they are convinced that component programming and especially STL will only be accepted when there is no (serious) loss of efficiency when using it.
Maybe there are users who can afford to work inefficiently but well designed - most can not.
The following table shows the insert and erase overheads of the containers vector, list and deque. Think of these overheads when choosing a container for solving a specific task.
Container insert/erase overhead in the middle at the end
at the beginning
Vector linear linear amortized
constant
List constant constant constant
Deque amortized linear amortized
constant constant
Table 3: Insert and erase overheads for vector, list and deque
Before we look at the insert functionality, there is another thing to consider. When a vector is constructed using the default constructor (the default constructor is used when no argument is given at the declaration), no memory for elements is allocated:
vector<int> v;
We can check this using the member function capacity(), which shows the number of elements for which memory has been allocated:
vector<int>::size_type capacity = v.capacity(); cout << "capacity:" << capacity;
Output: capacity: 0
turbine turb; turbine main_screen_turbines [max_size]; main_screen_turbines[0] = turb;
In STL you can use this syntax, too:
turbine turb;
vector<turbine> main_screen_turbines (10); // allocate memory for 10 elements
main_screen_turbines[0] = turb;
Now, we don't use the default constructor but specify a number that tells the vector for how many elements memory should be allocated. Then we use the overloaded subscribe operator (operator[] ) to insert a turbine object into the vector.
Note: If you use the subscribe operator with an index, for which no memory has been allocated (this is true for all indices when declaring a vector without specifying a vector size), the result will be undefined!
To avoid memory allocation stuff the vector provides different member functions to insert elements into the vector. These insert functions do automatic memory allocation and - if necessary - expansion. To append an element at the end of a vector use push_back():
vector<int> v; v.push_back (3); cout << v.capacity() << endl; cout << v[0];
Output: 2048
Output: 3
Note: The value 2048 depends on the environment (memory model) used
vector<int> v; v.insert (v.end(), 3); cout << v.capacity() << endl; cout << v[0];
Output: 2048
Output: 3
The element is inserted before the specified iterator-position, that is before the element the specified iterator points to.
The term iterator needs some explanation. There are two member functions which return so-called iterators: begin() and end().
Iterators are a generalization of the C++ pointers. An iterator is a kind of pointer but indeed more than a pointer. Like a pointer is dereferenced by the expression *pointer, an iterator has the dereference operator* defined which returns a value of a specific type - the value type of the iterator. Additionally, like a pointer can be incremented by using the operator++, an iterator can be incremented in the same way. Iterators most often are associated with a container. In that case, the value type of the iterator is the value type of the container and dereferencing the iterator returns an object of this value type. Look at this example to get a feeling how iterators behave:
vector<int> v(3); v[0] = 5; v[1] = 2; v[2] = 7; vector<int>::iterator first = v.begin(); vector<int>::iterator last = v.end(); while (first != last) cout << *first++ << " " ;
Output: 5 2 7
Please note, that v.end() doesn't return an iterator that points to the last element in the vector - as now could be supposed - but past the last element (however, in the STL code such an iterator is named last). Accordingly it is called past-the-end iterator. A user is not supposed to dereference such an iterator, because the result would be undefined. The while loop checks if the first iterator is equal to the last iterator. If not, the iterator is dereferenced to get the object it is pointing to, then it is incremented. So, all vector elements are written to cout.

Figure 5: Range specified by iterators
A range [i, j) given by the iterators i and j is valid, if j is reachable from i, that means if there is a finite sequence of applications of operator++ to i that makes i==j;
Ranges given by two iterators are very important in STL, because STL algorithms largely work in the following way:
sort (begin-iterator, past_the_end-iterator)
where begin-iterator specifies the first element in the range and past_the_end-iterator points past the last element of the range to be sorted.
The range is correctly specified by the expression [begin-iterator, past_the_end-iterator).
A valid sort command for our vector-example would be:
sort (v.begin(), v.end() );
Note: To use algorithms in your programs you have to include algo.h
Using iterators as intermediates, we are able to seperate the algorithms from the container implementations:
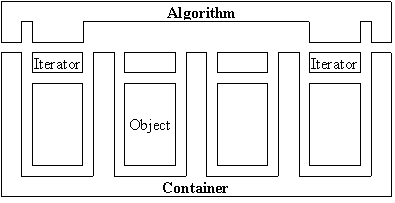
Figure 6: Orthogonal decomposition of the component space
After this short survey on iterators, which will be described in very detail in the next section, we focus on the vector container again.
We learned that specifying a number when declaring a vector reserves memory for elements. Additionally to that, you can give the elements for which memory is reserved an initial value:
vector<int> v(3, 17); for (int i = 0; i < 3; i++) cout << v[i] << " " ;
Output: 17 17 17
vector<float> v (5, 3.25); vector<float> v_new1 (v); // construct v_new1 out of v vector<float> v_new2 = v; // assign v to vnew2 // now construct v_new3 out of the elements of v vector<float> v_new3 (v.begin(), v.end() );
The last version uses iterators to specify the range out of which the v_new3 vector should be constructed. The three v_new - vectors are all equal:
(v_new1 == v_new2) && (vnew2 == v_new3) && (n_new1 == v_new3) ? cout << "equal" : cout << "different";
Output: equal
To swap two vectors, a special member function is provided which needs merely constant time, because only internal pointers are manipulated.
vector<int> v (1, 10); vector<int> w (1,20); v.swap (w); cout << v[0];
Output: 20
vector<char> v; v.empty() ? cout << "empty" : cout << "not empty";
Output: empty
vector<int> v (10, 5); v.push_back (7); cout << v.front() << " " << v.back();
Output: 5 7
vector<int> v (1, 2); int value = v.pop_back (); cout << value << endl; v.empty() ? cout << "empty" : cout << "not empty";
Output: 2
Output: empty
vector<int> v; v.insert (v.begin(), 2, 5); // vector v: 5 5 vector<int> w (1, 3); w.insert (w.end(), v.begin(), v.end() ); // vector w: 3 5 5
The second argument of the first version specifies how many copies of an element - given as third argument - should be inserted before the specified iterator-position (first argument). The second version takes additionally to the inserting position w.end() two iterators that specify the range which is to be inserted.
Using the erase() member function, it is possible to erase single elements or ranges (specified by two iterators) from a vector. Accordingly, there are two versions of erase(). Erasing at the end of the vector takes constant time whereas erasing in the middle takes linear time.
vector<float> v (4, 8.0); // vector v: 8.0 8.0 8.0 8.0 v.erase (v.begin() ); // vector v: 8.0 8.0 8.0 v.erase (v.begin(), v.end() ); // vector v:
The first version erases the first vector element. The second version erases all remaining elements so the vector gets empty.
When inserting in or erasing from a container, there is something to take into consideration. If you have an iterator pointing e.g. to the end of a vector and you insert an element at its beginning, the iterator to the end gets invalid. Only iterators before the insertion point remain valid. If no place is left and expansion takes place, all iterators get invalid. This is clear, because new memory is allocated, the elements are copied and the old memory is freed. Iterators aren't automatically updated and get invalid, that means the result of operations using such iterators is undefined. Take this into consideration when inserting or erasing and then using iterators earlier defined on this container. The following table shows the validity of the containers vector, list and deque after inserting and erasing an element, respectively.
Container operation iterator validity
vector inserting reallocation necessary- all iterators get invalid no reallocation - all iterators before insert point remain valid erasing all iterators after erasee point get invalid list inserting all iterators remain valid erasing only iterators to erased elements get invalid deque inserting all iterators get invalid erasing all iterators get invalid
Table 4: Iterator validity after inserting or erasing
Now we are able to store objects in a container (at least in the vector) that provides several means to administer and maintain it. To apply algorithms to the elements in the vector we have to understand the iterator concept which is described in detail in the next section.
I thought up a few exercises with solutions to show how STL can be applied.
Johannes Weidl (J.Weidl@infosys.tuwien.ac.at) - Apr 16, 1996