In the calculations detailed above (Equations 6 to 10),
![]() was obtained by convoluting the measured image by the smoothing function
was obtained by convoluting the measured image by the smoothing function
![]() , with the implication that it would be calculated by a Fourier transform
and subsequent point-wise multiplication of the two terms. However, if this
were the case we would have the subtle problem of Equation 10
being
, with the implication that it would be calculated by a Fourier transform
and subsequent point-wise multiplication of the two terms. However, if this
were the case we would have the subtle problem of Equation 10
being
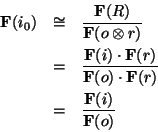
However, the reason for ![]() 's existence is that we can smooth
's existence is that we can smooth ![]() in real space, not Fourier space. This is achieved using a mask operation on
in real space, not Fourier space. This is achieved using a mask operation on
![]() , for example, using the convolution matrix of
, for example, using the convolution matrix of
![\begin{displaymath}
\left[ \begin{array}{ccc}
1 & 1 & 1\\
1 & 5 & 1\\
1 & 1 & 1
\end{array}\right] \end{displaymath}](img63.gif)
![\begin{displaymath}
\left[ \begin{array}{ccccc}
1 & 1 & 1 & 1 & 1\\
1 & 5 & 5 &...
...1\\
1 & 5 & 5 & 5 & 1\\
1 & 1 & 1 & 1 & 1
\end{array}\right] \end{displaymath}](img65.gif)
Again, this procedure will decrease the accuracy somewhat, but it will increase the speed of the algorithm substantially as this method is localized for each point, requiring only a constant amount of computational time per point, which is faster than any Fourier transform (refer to Section 4.1 for a complete analysis of the time complexity of the algorithm).