

Next: About this document ...
Up: Database Internals
Paper Presentation:
Robust Distance-Based Clustering
with Applications to Spatial Data Mining
by Vladimir Estivill-Castro and Michael Houle
to appear in 2000 in Algorithmica
height 7pt
KEVIN PULO
24 May 2000
[-0.5in]Spatial Data Mining
height 3pt
- Large spatial datasets of points.
- Too large to visualise.
- Possibly higher dimensional.
- Want to find sets of similar points within the dataset.
- Exploratory analysis desires techniques which are automatic and fast.
- Avoid human bias.
- Fast response times aid the exploration.
- Most common application is 2 dimensional spatial data in Geographical Information
Systems (GIS).
[-0.5in]Clustering Methods
height 3pt
- Clustering is a key technique in Spatial Data Mining.
- Good quality clustering algorithms are usually expensive, ie.
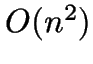 or worse.
or worse.
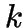 -MEANS is a simple clustering algorithm taking
-MEANS is a simple clustering algorithm taking 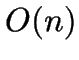 time.
time.
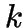 -MEDOIDS (
-MEDOIDS (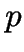 -median) is a more constrained
version of
-median) is a more constrained
version of 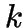 -MEANS, taking
-MEANS, taking
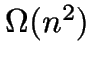 time.
time.
- The paper presents a variant of a
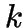 -MEDOIDS heuristic,
using the Delaunay triangulation to require only
-MEDOIDS heuristic,
using the Delaunay triangulation to require only 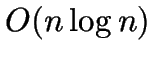 time.
time.
[-0.5in]Clustering
height 3pt
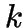 clusters, each represented by a representative point.
clusters, each represented by a representative point.
- The most appropriate number of clusters
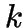 may or may not be determined
by the algorithm.
may or may not be determined
by the algorithm.
- Representative point may or may not be a data point of the dataset.
- Points need not belong to a cluster, eg. noise and outlier points.
- Clustering algorithms give approximate solutions to the problem of minimising
the sum of the distances of each data point from their nearest representative
point.
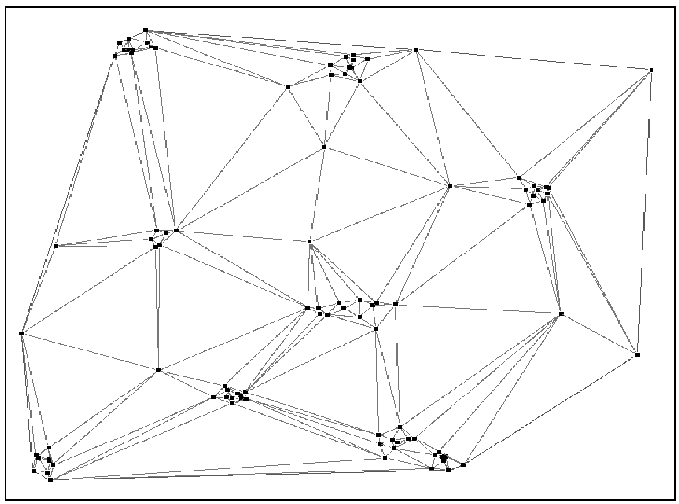
[-0.5in]Sample Dataset
height 3pt
Sample points lying in the 2 dimensional
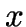
-
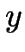
plane.
[-0.5in]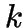 -MEANS
-MEANS
height 3pt
- Take an initial (perhaps random) clustering.
- For each cluster, find the new representative by computing the average of the
cluster points.
- Using these new representatives, find a new clustering (ie. assign points to
their nearest, possibly different, representative).
- Repeat these two steps until no change occurs.
- This is ``non-combinatorial'' reclassification, the ``combinatorial'' reclassification
variant recomputes the clustering each time a new representative is computed.
[-0.5in]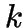 -MEANS:
-MEANS:
Advantages and Disadvantages
height 3pt
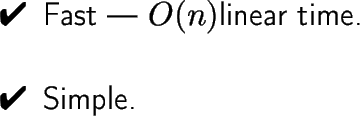

[-0.5in] -MEDOIDS
-MEDOIDS
height 3pt
Similar to  -MEANS, but has the additional restriction that
the representative points must be chosen from the set of data points.
-MEANS, but has the additional restriction that
the representative points must be chosen from the set of data points.
The TB heuristic, by Teitz and Bart, 1968, is the best known benchmark:
- Maintains a selection of
 representative points from the
representative points from the 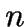 data
points.
data
points.
- Considers the data points in a fixed circular ordering
 .
.
- If
 is a representative, it is skipped, otherwise, it considers
interchanging
is a representative, it is skipped, otherwise, it considers
interchanging 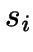 with
with 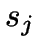 , for all possible representatives
, for all possible representatives
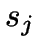 .
.
- If any of these yield an improvement, the interchange is performed, and the
search continues from
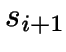 .
.
- The search stops with a local optimum when a full cycle of the data points gives
no improvement.
The number of points considered for interchange per iteration is typically constant.
However, all 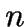 points must be examined for termination.
points must be examined for termination.
The circular ordering of points balances the need to explore various interchanges
against the greed of improving the solution quickly.
[-0.5in]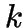 -MEDOIDS:
-MEDOIDS:
Advantages and Disadvantages
height 3pt


[-0.5in]Delaunay Triangulation
height 3pt
Delaunay triangulations succinctly encapsulate the proximity information of
a set of points.
- Points
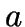 and
and 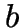 are joined by the Delaunay
edge
are joined by the Delaunay
edge 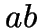 iff they are ``nearest neighbours''.
iff they are ``nearest neighbours''.
- Delaunay edge
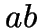
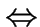
 some circle
through
some circle
through 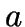 and
and 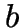 containing no other points.
containing no other points.
- For
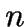 data points, at most
data points, at most 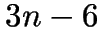 edges.
edges.
- Average number of neighbours of a point is less than 6.
- Minimum angle of all triangles is the maximum possible.
- Robust computation in
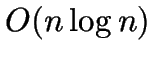 time.
time.
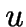 nearest neighbours of a point found in
nearest neighbours of a point found in 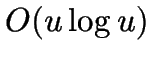 time.
time.
[-0.5in]Sample Dataset:
Delaunay Triangulation
height 3pt
Sample points lying in the 2 dimensional
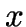
-
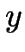
plane
and their Delaunay triangulation.
[-0.5in]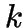 -MEDOIDS Delaunay Variant
-MEDOIDS Delaunay Variant
height 3pt
- Evaluating
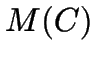 exactly requires
exactly requires 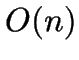 time per interchange possibility.
time per interchange possibility.
- Greatest contribution to
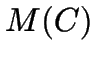 is made by outliers (and initially there
are more outlying representatives).
is made by outliers (and initially there
are more outlying representatives).
- Increase performance not by limiting the points examined by TB, but by approximating
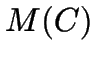 with
with 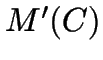 .
.
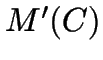 considers only the
considers only the  nearest neighbours, precomputed for
all points in
nearest neighbours, precomputed for
all points in 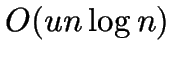 time using the Delaunay triangulation.
time using the Delaunay triangulation.
- Evaluating
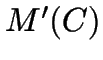 takes only
takes only 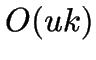 time per interchange possibility.
time per interchange possibility.
- If
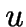 is chosen to be
is chosen to be
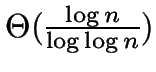 , then
the overall time bound simplifies to
, then
the overall time bound simplifies to 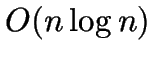 . The choice of
. The choice of 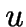 determines a speed-quality tradeoff.
determines a speed-quality tradeoff.
[-0.5in]Sample Dataset:
Clustering Results
height 3pt
The clustering of sample points produced by the algorithm.
[-0.5in]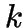 -MEDOIDS Delaunay Variant:
-MEDOIDS Delaunay Variant:
Advantages and Disadvantages
height 3pt


[-0.5in]Finding an Initial Clustering
height 3pt
The following method is used to find the initial clustering in 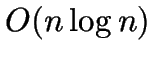 time.
time.
- Put each data point into its own set.
- Sort the edges of the Delaunay triangulation by increasing length.
- For each edge, merge the sets connected by its endpoints.
- Stop when
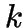 sets of size at least
sets of size at least 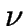 (say, 2 or 3) remain.
(say, 2 or 3) remain.
- These sets form the initial clustering, representatives are chosen arbitrarily
from them.
This technique maximises the minimum distance between initial clusters.
[-0.5in]Finding 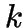 Automatically
Automatically
height 3pt
This method can be adapted to find a suitable value of 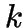 for the dataset
in
for the dataset
in 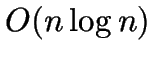 time.
time.
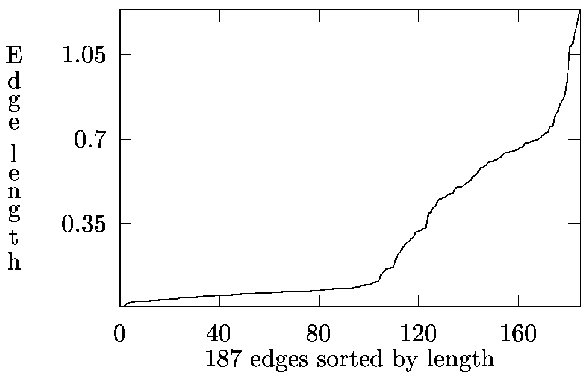
Consider the profile of sorted edge lengths.
Merge sets as before until just before the inflexion point, these are all the
short edges which are ``obviously'' within clusters.
The number of sets of size at least 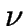 is then taken as
is then taken as 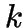 , and
the initial representatives chosen from these
, and
the initial representatives chosen from these 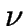 sets.
sets.
[-0.5in]Comparison with Other
Subquadratic Algorithms
height 3pt
[-0.5in]Experiments
height 3pt
[-0.5in]Blank Slide
height 3pt


Next: About this document ...
Up: Database Internals
Kevin Pulo
2000-08-23
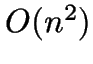 or worse.
or worse.
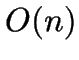 time.
time.
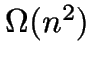 time.
time.
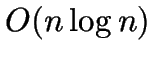 time.
time.
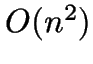 or worse.
or worse.
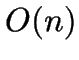 time.
time.
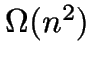 time.
time.
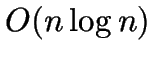 time.
time.
![\begin{displaymath}
\textrm{minimise }M(C)=\sum ^{n-1}_{i=0}d(s_{i},\textrm{rep}[s_{i},C])\end{displaymath}](img7.gif)

![]() -MEANS
-MEANS
![]() -MEANS:
-MEANS:

![]() -MEDOIDS
-MEDOIDS
![]() -MEANS, but has the additional restriction that
the representative points must be chosen from the set of data points.
-MEANS, but has the additional restriction that
the representative points must be chosen from the set of data points.
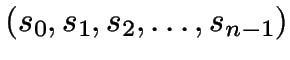 .
.
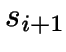 .
.
![]() -MEDOIDS:
-MEDOIDS:


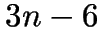 edges.
edges.
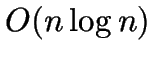 time.
time.
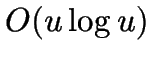 time.
time.
![]() -MEDOIDS Delaunay Variant
-MEDOIDS Delaunay Variant
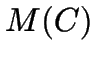 exactly requires
exactly requires  time per interchange possibility.
time per interchange possibility.
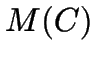 is made by outliers (and initially there
are more outlying representatives).
is made by outliers (and initially there
are more outlying representatives).
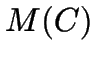 with
with 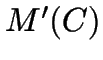 .
.
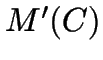 considers only the
considers only the 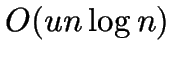 time using the Delaunay triangulation.
time using the Delaunay triangulation.
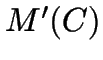 takes only
takes only 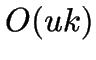 time per interchange possibility.
time per interchange possibility.
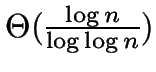 , then
the overall time bound simplifies to
, then
the overall time bound simplifies to 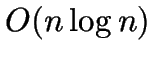 . The choice of
. The choice of 
![]() -MEDOIDS Delaunay Variant:
-MEDOIDS Delaunay Variant:


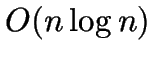 time.
time.
![]() Automatically
Automatically
![]() for the dataset
in
for the dataset
in 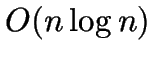 time.
time.
![]() is then taken as
is then taken as ![]() , and
the initial representatives chosen from these
, and
the initial representatives chosen from these ![]() sets.
sets.
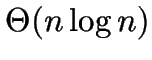 expected
expected


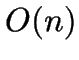 construction,
construction, 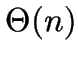 queries
queries

